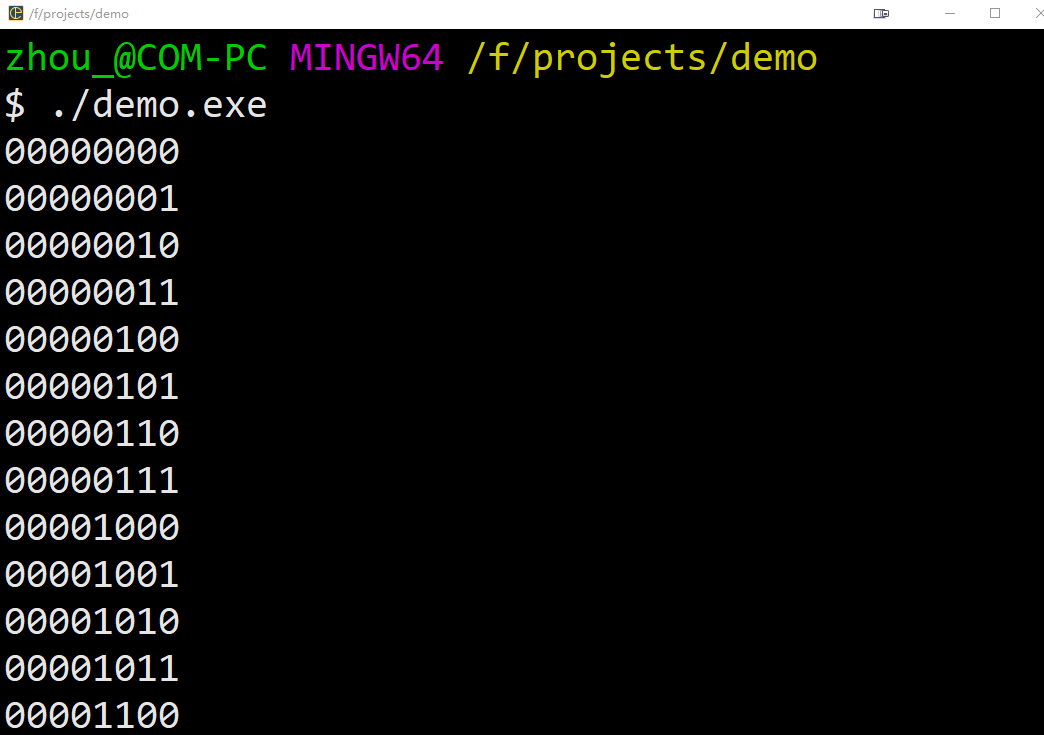
之前的章节中,我们对于数据的操作最小单位为字节,每个字节由8个二进制位组成。这一节中,我们深入到字节的内部,讨论如何直接操作字节内部的二进制位。
1. 十进制转二进制
工欲善其事必先利其器。
生物学家研究细胞需要使用显微镜才能观察到细胞的结构,天文学家需要望远镜才能观察到遥远的天体。而我们研究字节中的二进制,也需要有一种手段观察到字节内的二进制组成。
短除法
对于将十进制数据转为二进制数据,我们可以使用短除法。
例如:需要将十进制42转为二进制。算法如下:
- 被除数
42,在其左下角打上符号|___,表示将对其进行短除运算。 - 符号
|___左边写上除数2。 -
计算被除数除以除数的商和余数。
42 / 2 = 21 ... 0。 - 将商
21填到符号|___下面,余数0填到右侧。
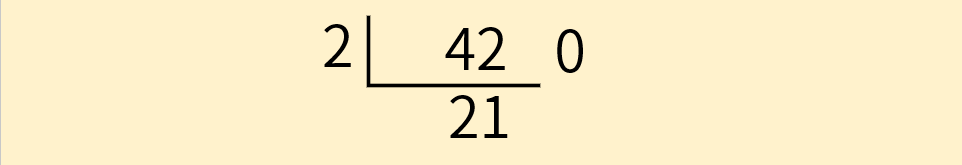
现在我们已经计算过一次短除了,下面将商作为新的被除数,重复上述步骤。
- 被除数
21,在其左下角打上符号|___,表示将对其进行短除运算。 - 符号
|___左边写上除数2。 -
计算被除数除以除数的商和余数。
21 / 2 = 10 ... 1。 - 将商
10填到符号|___下面,余数1填到右侧。
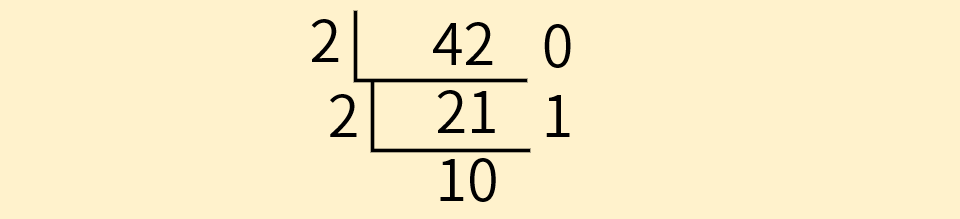
接着,继续将商作为新的被除数,重复上述步骤,直到商为0为止。
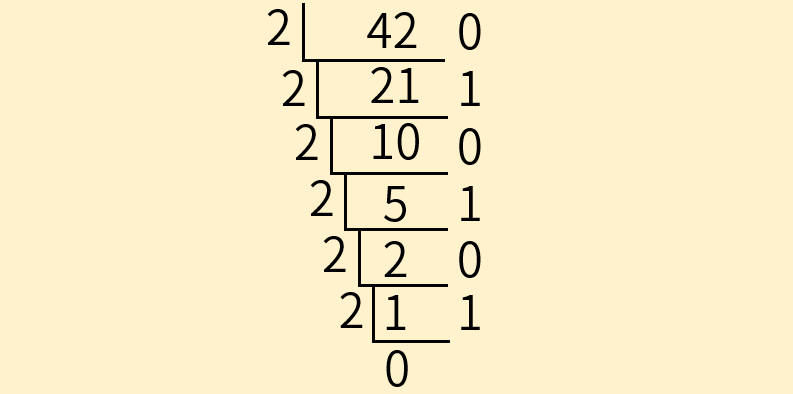
最后,若我们希望先读高位、后读低位。从下往上逆序读右侧的余数101010。这就是十进制数42所对应的二进制。
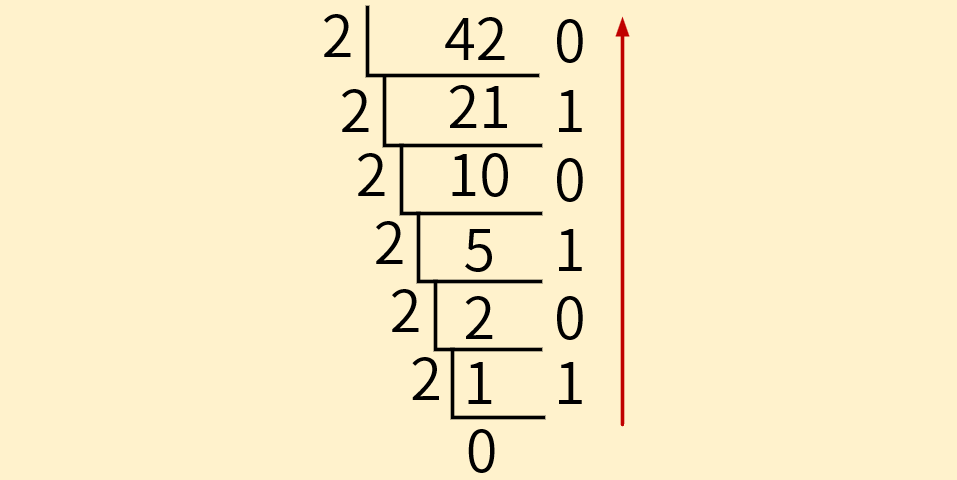
现在,我们再把这个二进制转换回十进制,验算一下是否等于42。
将二进制转换为十进制,可以把二进制中的各位乘以其所在位的位权,再将所有乘法的积累加起来,即可得到转换后的十进制结果。
例如:
二进制101010,高位在左,低位在右。
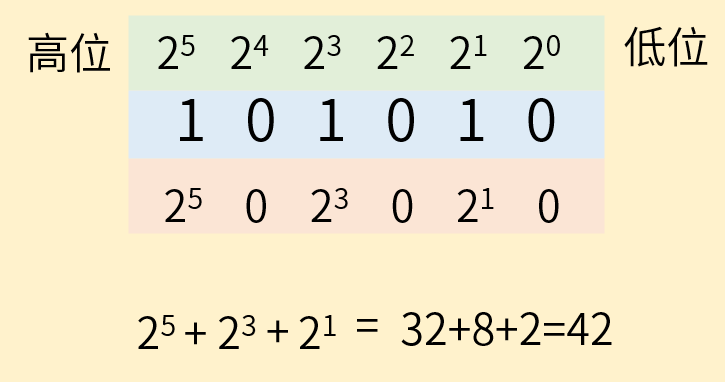
最低位的位权为2的0次方,此后的位权依次加1次方。高位具有更大的位权,低位具有较小的位权。
从最高位开始:
- 第1位的位权为,该位为1,积为。
- 第2位的位权为,该位为0,积为。
- 第3位的位权为,该位为1,积为。
- 第4位的位权为,该位为0,积为。
- 第5位的位权为,该位为1,积为。
- 第6位的位权为,该位为0,积为。
将所有的乘法的积累加起来,那么其十进制为:
2^5 + 2^3 + 2^1 = 32 + 8 + 2 = 422. 十进制转二进制函数
现在我们将十进制转二进制的步骤写成程序。尝试写一个函数printBinary,它能将传入的数据转换为二进制并打印出来。暂时限制二进制位最多为8位,即传入的参数为unsigned char类型。
void printBinary(unsigned char dec)
{
unsigned int quotient; // 商
unsigned int remainder; // 余数
while(dec > 0)
{
// 求除2的余数
remainder = dec % 2;
// 求除2的商
quotient = dec / 2;
// 输出商
printf("%d", remainder);
// 商作为新的被除数
dec = quotient;
}
putchar('\n');
}
变量dec为短除运算中的被除数。变量quotient用于放置除2的商。变量remainder用于放置除2的余数。计算完毕后,使用printf输出余数,并且把商作为新的被除数,再次进行短除运算,直到被除数为0为止。
将十进制数42作为参数传入函数printBinary。
printBinary(42);运行后,结果为010101。由于代码中顺序输出余数,所以输出结果为:低位在前,高位在后。
若希望高位在前,低位在后,需要逆序输出每一次计算的余数。
对于参数dec来说,它是一个unsigned char类型的变量,长1字节,拥有8位二进制。可以使用一个有8个元素的数组char bits[8]来存储二进制位,每个元素分别保存每一位的二进制状态。现在,计算出余数之后,不直接输出,而是存储到bits数组的count下标的元素当中。之后,count加1,新的余数将被存储在下一个元素当中。
void printBinary(unsigned char dec)
{
// 存储dec的每一位二进制状态
char bits[8];
int count = 0;
int quotient; // 商
int remainder; // 余数
while(dec > 0)
{
// 求除2的余数
remainder = dec % 2;
// 求除2的商
quotient = dec / 2;
// 商作为新的被除数
dec = quotient;
// 将余数保存到bits
bits[count] = remainder;
count++;
}
// 逆序输出有数据的二进制位
for (int i = count - 1; i >= 0; i--)
printf("%d", bits[i]);
}
循环结束后,count个二进制被存储到bits数组当中。从数组的count - 1下标开始,逆序输出这些二进制位,直到下标0为止,即可得到从高位到低位的转换结果。

如果参数dec为0呢?dec为0时,无法进入循环while(dec > 0),将没有任何输出。对于参数dec为0的情况可以做一个特殊处理。若dec为0,那么直接输出0并将函数返回。
void printBinary(unsigned char dec)
{
// 若dec为0,输出0并返回
if (dec == 0)
{
printf("0\n");
return;
}
// 若dec非0,短除计算余数,逆序输出
char bits[8];
int count = 0;
int quotient;
int remainder;
while(dec > 0)
{
remainder = dec % 2;
quotient = dec / 2;
dec = quotient;
bits[count] = remainder;
count++;
}
for (int i = count - 1; i >= 0; i--)
printf("%d", bits[i]);
putchar('\n');
}
对于unsigned char类型的变量dec来说,它拥有8个二进制位。而十进制数42,只占6个二进制位,还有两个二进制位为0。若需要把8个二进制位全部输出,可以将bits数组初始化为0。计算完余数后,从数组的最后一个元素开始,逆序输出直到数组第一个元素。此时,无需对dec为0做特殊处理了。由于数组bits初始化为0,dec为0时,不进入while循环,直接输出8个0。
void printBinary(unsigned char dec)
{
// 数组初始化为0
char bits[8] = {0};
int count = 0;
int quotient;
int remainder;
while(dec > 0)
{
remainder = dec % 2;
quotient = dec / 2;
dec = quotient;
bits[count] = remainder;
count++;
}
// 逆序输出所有二进制位
for (int i = 8 - 1; i >= 0; i--)
printf("%d", bits[i]);
putchar('\n');
}这样,数据二进制最高位前的两个零也被打印出来了。
测试一下,从0到16的十进制能否转为对应二进制呢?
for(int i = 0; i <= 16; i ++)
{
printBinary(i);
}