在动画那一节当中,我们实现了直线运动中的水平和垂直运动。这一节中,我们来讨论更加普遍的直线运动。
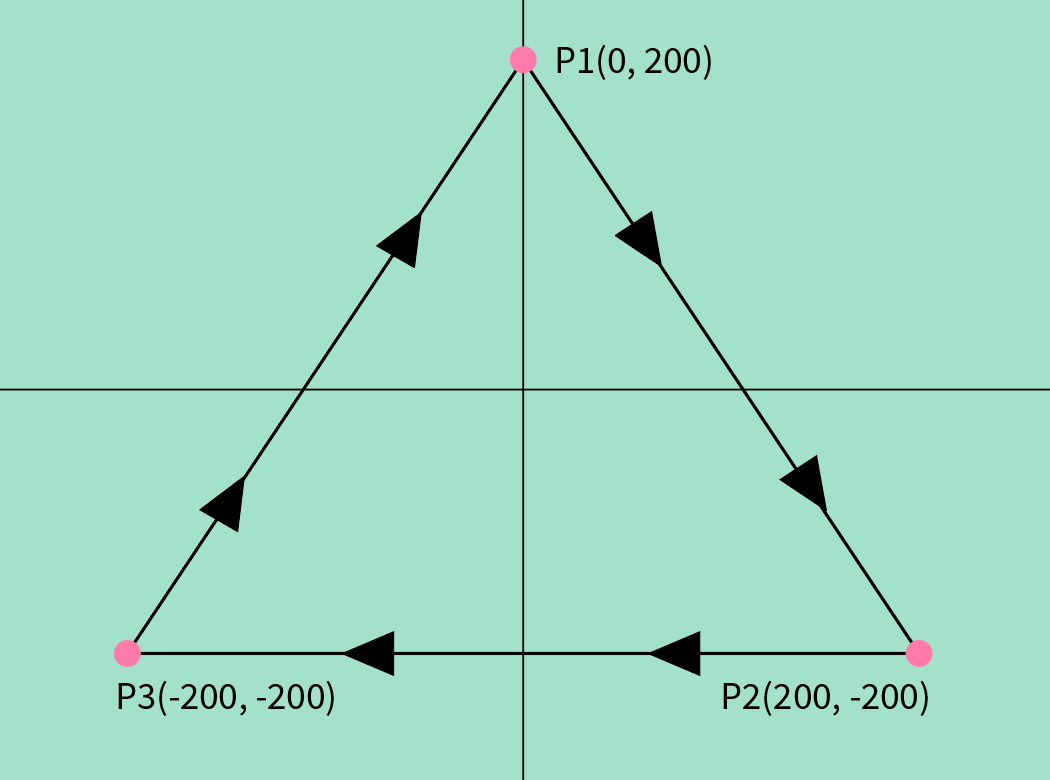
画面中有3个点:
- P1(0, 200)
- P2(200, -200)
- P3(200, -200)
以这三个顶点围成一个三角形,让一个圆形沿着这个三角形的边缘以125像素/s,每秒25帧运动。
在这之前,我们先把窗体和坐标系设置好。
创建一个800 * 600的窗体。坐标系原点在窗体中心,x轴正方向向右,y轴正方向向上。背景色设置为RGB(164, 225, 202),最后调用cleardevice函数,使用背景色清空整个窗体。
#include <easyx.h>
#include <stdio.h>
#include <math.h>
int main()
{
initgraph(800, 600);
// 坐标系原点在窗体中心,X轴正方向向右,Y轴正方向向上
setorigin(400, 300);
setaspectratio(1, -1);
// 设置背景色
setbkcolor(RGB(164, 225, 202));
// 使用背景色清空窗体
cleardevice();
getchar();
closegraph();
return 0;
}1. P1到P2
圆形从P1运动到P2。由于是直线运动,速度与位移的方向是相同的,均是从P1到P2。此时,速度方向并不是水平或垂直的。但是,我们可以通过三角函数计算出速度在x方向与y方向的速度分量。为了计算出速度分量,还需要先求出速度方向与x轴的夹角。
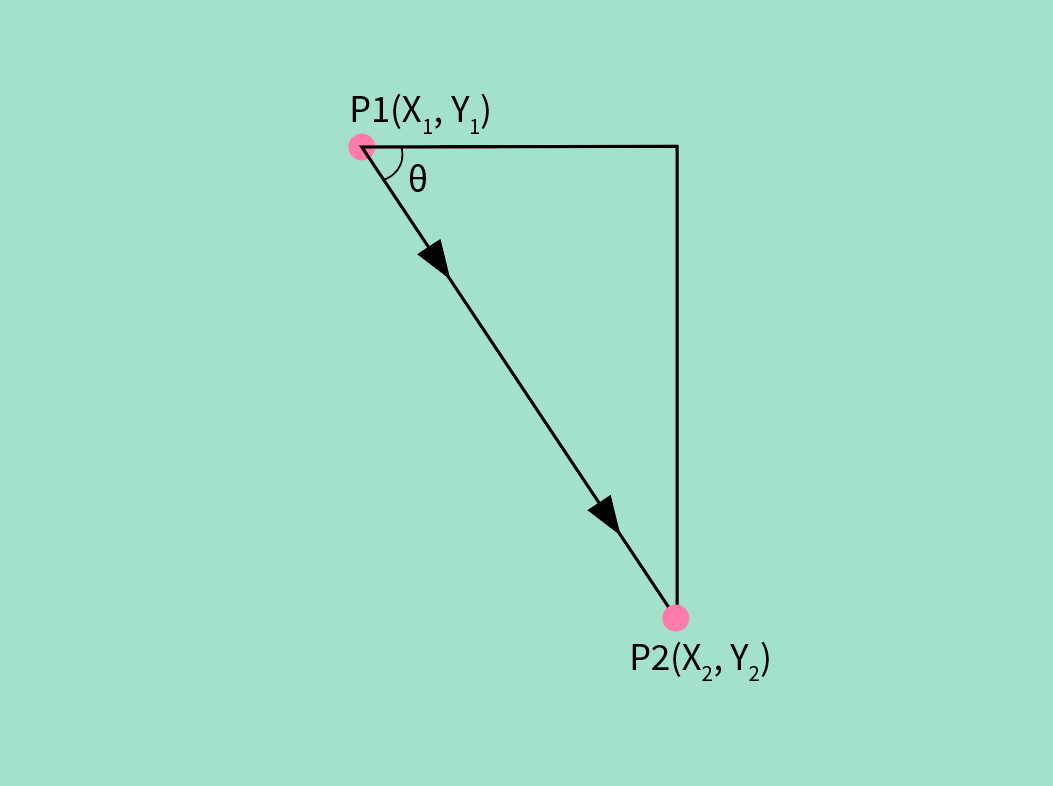
设P1点的坐标为(X1, Y1), P2点的坐标为(X2, Y2)。可求得。
将传入反三角函数,可求得。
// 起始点(x1, y1),终止点(x2, y2)
int x1, y1, x2, y2;
// 起始点为(0, 200)
x1 = 0;
y1 = 200;
// 终止点为(200, -200)
x2 = 200;
y2 = -200;
// 计算角度θ的正切tanTheta
double tanTheta = (double)abs(y2 - y1) / (double)abs(x2 - x1);
// 已知tanTheta,根据反三角函数计算角度θ
double theta = atan(tanTheta);设速度为v,又知道了速度与x轴的夹角,可将速度分解为x方向的分量vx与y方向的vy分量。
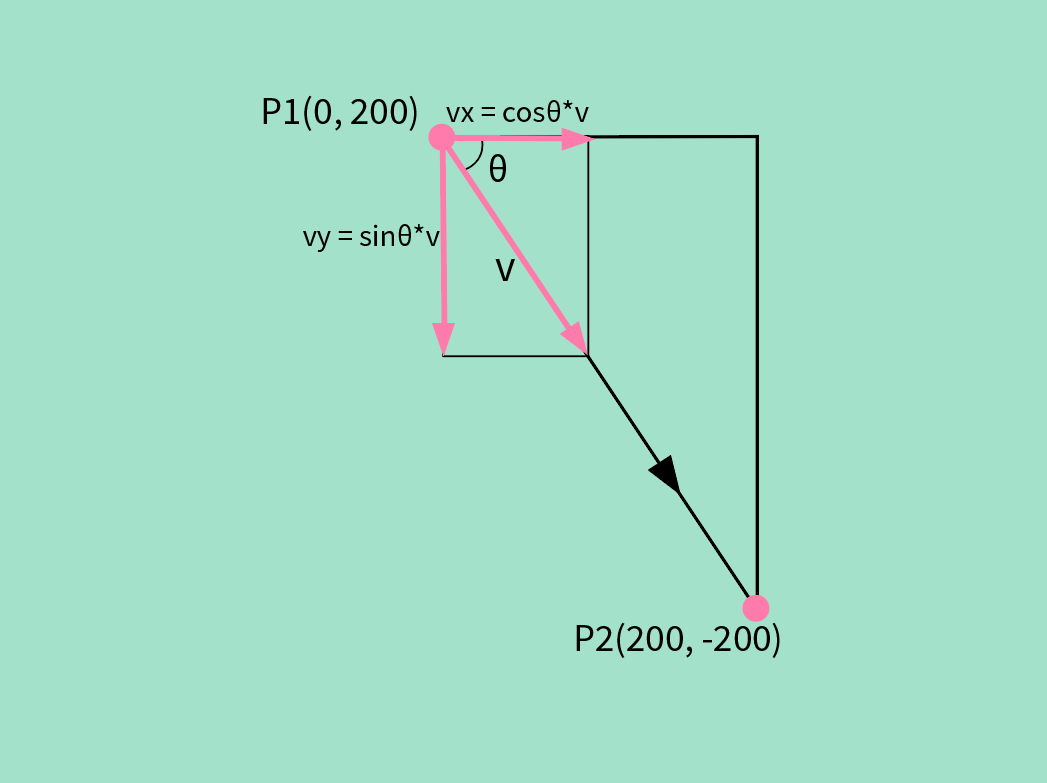
设速度为125像素/s,帧率为25帧每秒。则每帧之间的速度为125 / 25 = 5像素/帧。